Геометрия

Геометрия	Методическая копилка
Прямые и плоскости в пространстве
Занятие 1 .	Взаимное расположение двух прямых в пространстве.
Занятие 2	Признак параллельности прямой и плоскости.
Занятие 3	Взаимное расположение двух плоскостей.
Занятие 4	Теорема о трёх перпендикулярах.
Занятие 5	Двугранный угол. Линейный угол двугранного угла.
Многогранники
Занятие 6	Понятие о многограннике. Правильные многогранники.
Занятие 7	Прямая и правильная призма. Параллелепипед.
Занятие 8	Пирамида. Усечённая пирамида.
Занятие 9	Решение задач по теме "Многогранники".
Тела и поверхности вращения
Занятие 10	Тела и поверхности вращения
Занятие 11	Цилиндр. Конус.
Занятие 12	Сфера. Шар.
Объемы тел и площади их поверхности
Занятие 13	Объём параллелепипеда, призмы, цилиндра, пирамиды и конуса.
Занятие 14	Площади поверхностей призмы, пирамиды, цилиндра и конуса.
Занятие 15	Объём шара и его частей. Площадь сферы.
Координаты и векторы.
Занятие 16	Координаты вектора. Скалярное произведение векторов.
Занятие 17	Угол между векторами.
Занятие 18	Векторное произведение векторов.

Занятие 3. Взаимное расположение двух плоскостей.

Две плоскости могут быть параллельны друг другу или пересекаться одна с другой.

1. Параллельные плоскости

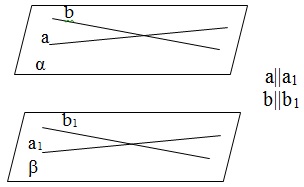
Определение. Две плоскости называются параллельными, если они не пересекаются, то есть не имеют общих точек.

Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Теорема. Через точку вне данной плоскости можно провести плоскость, параллельную данной и притом только одну.

2. Пересекающиеся плоскости

Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям.

Свойства параллельных плоскостей

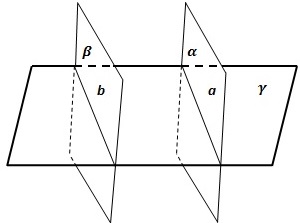
1) Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
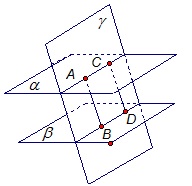
2) Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.
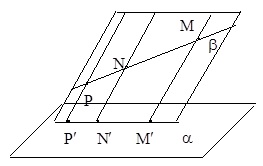
3) Отношение отрезков одной прямой или параллельных прямых сохраняется при параллельном проектировании.

Номера для работы на занятии

№27 страница 21, кроссворды

Контрольные вопросы на странице 18

Домашнее задание

Проект на тему: «В мире прямых и плоскостей»